您现在的位置是: 首页 > 教育改革 教育改革
杭州2017高考模拟数学_2017杭州市中考数学试卷答案
tamoadmin 2024-05-31 人已围观
简介1.2017江苏高考数学太难考生痛哭 被葛军支配的恐惧2.2017高考状元事迹_2017高考状元事迹有哪些一、选择题 1.平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,点D在直线3x-y+1=0上移动,则点B的轨迹方程为( ) A.3x-y-20=0 B.3x-y+10=0 C.3x-y-9=0 D.3x-y-12=0 答案:A 解题思路:设AC的中点为O,即.设B(
1.2017江苏高考数学太难考生痛哭 被葛军支配的恐惧
2.2017高考状元事迹_2017高考状元事迹有哪些

一、选择题
1.平行四边形ABCD的一条对角线固定在A(3,-1),C(2,-3)两点,点D在直线3x-y+1=0上移动,则点B的轨迹方程为( )
A.3x-y-20=0 B.3x-y+10=0
C.3x-y-9=0 D.3x-y-12=0
答案:A 解题思路:设AC的中点为O,即.设B(x,y)关于点O的对称点为(x0,y0),即D(x0,y0),则由3x0-y0+1=0,得3x-y-20=0.
2.由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值为( )
A.1 B.2
C. -2D.3
答案:C 解题思路:当该点是过圆心向直线引的垂线的交点时,切线长最小.因圆心(3,0)到直线的距离为d==2,所以切线长的最小值是l==.
3.直线y=x+b与曲线x=有且只有一个交点,则b的取值范围是( )
A.{b||b|=}
B.{b|-1
C.{b|-1≤b<1}
D.非以上答案
答案:
B 解题思路:在同一坐标系中,画出y=x+b与曲线x=(就是x2+y2=1,x≥0)的图象,如图所示,相切时b=-,其他位置符合条件时需-1
4.若圆C:x2+y2+2x-4y+3=0关于直线2ax+by+6=0对称,则由点(a,b)向圆所作的切线长的最小值是( )
A.2 B.3
C.4 D.6
答案:C 解题思路:圆的标准方程为(x+1)2+(y-2)2=2,所以圆心为(-1,2),半径为.因为圆关于直线2ax+by+6=0对称,所以圆心在直线2ax+by+6=0上,所以-2a+2b+6=0,即b=a-3,点(a,b)到圆心的距离为
d==
==.
所以当a=2时,d有最小值=3,此时切线长最小,为==4,故选C.
5.已知动点P到两定点A,B的距离和为8,且|AB|=4,线段AB的中点为O,过点O的所有直线与点P的轨迹相交而形成的线段中,长度为整数的有( )
A.5条 B.6条
C.7条 D.8条
答案:D 命题立意:本题考查椭圆的定义与性质,难度中等.
解题思路:依题意,动点P的轨迹是以A,B为焦点,长轴长是8,短轴长是2=4的椭圆.注意到经过该椭圆的中心O的最短弦长等于4,最长弦长是8,因此过点O的所有直线与点P的轨迹相交而形成的线段中,长度可以为整数4,5,6,7,8,其中长度为4,8的各一条,长度为5,6,7的各有两条,因此满足题意的弦共有8条,故选D.
6.设m,nR,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则m+n的取值范围是( )
A.[1-,1+]
B.(-∞,1-][1+,+∞)
C.[2-2,2+2]
D.(-∞,2-2][2+2,+∞)
答案:D 解题思路: 直线与圆相切,
=1,
|m+n|=,
即mn=m+n+1,
设m+n=t,则mn≤2=,
t+1≤, t2-4t-4≥0,
解得:t≤2-2或t≥2+2.
7.在平面直角坐标系xOy中,设A,B,C是圆x2+y2=1上相异三点,若存在正实数λ,μ,使得=λ+μ,则λ2+(μ-3)2的取值范围是( )
A.[0,+∞) B.(2,+∞)
C.(2,8) D.(8,+∞)
答案:B 解题思路:依题意B,O,C三点不可能在同一直线上, ·=|cos BOC=cos BOC∈(-1,1),又由=λ+μ,得λ=-μ,于是λ2=1+μ2-2μ·,记f(μ)=λ2+(μ-3)2.则f(μ)=1+μ2-2μ·+(μ-3)2=2μ2-6μ-2μ·+10,可知f(μ)>2μ2-8μ+10=2(μ-2)2+2≥2,且f(μ)<2μ2-4μ+10=2(μ-1)2+8无值,故λ2+(μ-3)2的取值范围为(2,+∞).
8.已知圆C:x2+y2=1,点P(x0,y0)在直线x-y-2=0上,O为坐标原点,若圆C上存在一点Q,使得OPQ=30°,则x0的取值范围是( )
A.[-1,1] B.[0,1]
C.[-2,2] D.[0,2]
答案:D 解析:由题知,在OPQ中,=,即=, |OP|≤2,又P(x0,x0-2),则x+(x0-2)2≤4,解得x0[0,2],故选D.
9.过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分成两部分,使得这两部分的面积之差,则该直线的方程为( )
A.x+y-2=0 B.y-1=0
C.x-y=0 D.x+3y-4=0
答案:A 命题立意:本题考查直线、线性规划与圆的综合运用及数形结合思想,难度中等.
解题思路:要使直线将圆形区域分成两部分的面积之差,必须使过点P的圆的弦长达到最小,所以需该直线与直线OP垂直.又已知点P(1,1),则kOP=1,故所求直线的斜率为-1.又所求直线过点P(1,1),故由点斜式得,所求直线的方程为y-1=-(x-1),即x+y-2=0.
10.直线y=kx+3与圆(x-2)2+(y-3)2=4相交于M,N两点,若|MN|≥2,则k的取值范围是( )
A. B.
C.[-, ] D.
答案:B 命题立意:本题考查直线与圆的位置关系,难度中等.
解题思路:在由弦心距d、半径r和半弦长|MN|构成的直角三角形中,由勾股定理,得|MN|=≥,得4-d2≥3,解得d2≤1,又d==,解得k2≤,所以-≤k≤.
二、填空题
11.已知直线l:y=-(x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则MOA的面积等于________.
答案: 命题立意:本题考查直线与圆的位置关系的应用,难度较小.
解题思路:联立直线与圆的方程可得xM=,故SMOA=×|OA|×xM=××=.
12.在ABC中,角A,B,C的对边分别为a,b,c.若a2+b2=c2,则直线ax-by+c=0被圆x2+y2=9所截得的弦长为________.
答案:2 命题立意:本题考查直线与圆位置关系的应用,求解弦长一般采用几何法求解,难度较小.
解题思路:圆心到直线的距离d===,故直线被圆截得的弦长为2=2=2.
13.已知A(-2,0),B(1,0)两点,动点P不在x轴上,且满足APO=BPO,其中O为原点,则点P的轨迹方程是________.
答案:(x-2)2+y2=4(y≠0) 命题立意:本题考查角平分线的性质及直接法求轨迹方程,难度中等.
解题思路:因为A(-2,0),B(1,0)两点,动点P不在x轴上,且满足APO=BPO,故点P在角APB的角平分线上,则利用PAPB=AOOB=21,设点P(x,y),则利用关系式可知=2化简可得(x-2)2+y2=4(y≠0).
14.若直线m被两平行线l1:x-y+1=0与l2:x-y+3=0所截得的线段的长为2,则m的倾斜角可以是
15° 30° 45° 60° 75°
其中正确答案的序号是________.(写出所有正确答案的序号)
答案: 解题思路:设直线m与l1,l2分别交于A,B两点,
过A作ACl2于C,则|AC|==.
又|AB|=2,ABC=30°.
又直线l1的倾斜角为45°,
直线m的倾斜角为45°+30°=75°或45°-30°=15°.
B组
一、选择题
1.已知抛物线C:y2=4x的焦点为F,直线y=2x-4与C交于A,B两点,则cos AFB=( )
A. B.
C.- D.-
答案:D 解题思路:联立消去y得x2-5x+4=0,解得x=1或x=4.
不妨设点A在x轴下方,所以A(1,-2),B(4,4).
因为F(1,0),所以=(0,-2),=(3,4).
因此cos AFB=
==-.故选D.
2.已知抛物线x2=4y上有一条长为6的动弦AB,则AB的中点到x轴的最短距离为( )
A. B.
C.1 D.2
答案:D 解题思路:由题意知,抛物线的准线l为y=-1,过A作AA1l于A1,过B作BB1l于B1,设弦AB的中点为M,过M作MM1l于M1,则|MM1|=,|AB|≤|AF|+|BF|(F为抛物线的焦点),即|AF|+|BF|≥6,即|AA1|+|BB1|≥6,即2|MM1|≥6, |MM1|≥3,即M到x轴的距离d≥2,故选D.
3.设双曲线-=1(a>0,b>0)的左、右焦点分别为F1,F2,A是双曲线渐近线上的一点,AF2F1F2,原点O到直线AF1的距离为|OF1|,则渐近线的斜率为( )
A.或- B.或-
C.1或-1 D.或-
答案:D 命题立意:本题考查了双曲线的几何性质的探究,体现了解析几何的数学思想方法的巧妙应用,难度中等.
解题思路:如图如示,不妨设点A是第一象限内双曲线渐近线y=x上的一点,由AF2F1F2,可得点A的坐标为,又由OBAF1且|OB|=|OF1|,即得sin OF1B=,则tan OF1B=,即可得=, =,得=,由此可得该双曲线渐近线的斜率为或-,故应选D.
4.设F1,F2分别是椭圆+=1(a>b>0)的左、右焦点,与直线y=b相切的F2交椭圆于点E,E恰好是直线EF1与F2的切点,则椭圆的离心率为( )
A. B.
C. D.
答案:C 解题思路:由题意可得,EF1F2为直角三角形,且F1EF2=90°,
|F1F2|=2c,|EF2|=b,
由椭圆的定义知|EF1|=2a-b,
又|EF1|2+|EF2|2=|F1F2|2,
即(2a-b)2+b2=(2c)2,整理得b=a,
所以e2===,故e=,故选C.
5.等轴双曲线C的中心在原点,焦点在x轴上,C与抛物线y2=16x的准线交于A,B两点,|AB|=4,则C的实轴长为( )
A. B.2 C.4 D.8
答案:C 解题思路:由题意得,设等轴双曲线的方程为-=1,又抛物线y2=16x的准线方程为x=-4,代入双曲线的方程得y2=16-a2y=±,所以2=4,解得a=2,所以双曲线的实轴长为2a=4,故选C.
6.抛物线y2=-12x的准线与双曲线-=1的两条渐近线围成的三角形的面积等于( )
A. B.3 C. D.3
答案:B 命题立意:本题主要考查抛物线与双曲线的性质等基础知识,意在考查考生的运算能力.
解题思路:依题意得,抛物线y2=-12x的准线方程是x=3,双曲线-=1的渐近线方程是y=±x,直线x=3与直线y=±x的交点坐标是(3,±),因此所求的三角形的面积等于×2×3=3,故选B.
7.若双曲线-=1与椭圆+=1(m>b>0)的离心率之积大于1,则以a,b,m为边长的三角形一定是( )
A.等腰三角形 B.直角三角形
C.锐角三角形 D.钝角三角形
答案:D 解题思路:双曲线的离心率为e1=,椭圆的离心率e2=,由题意可知e1·e2>1,即b2(m2-a2-b2)>0,所以m2-a2-b2>0,即m2>a2+b2,由余弦定理可知三角形为钝角三角形,故选D.
8. F1,F2分别是双曲线-=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左、右两支分别交于A,B两点.若ABF2是等边三角形,则该双曲线的离心率为( )
A.2 B. C. D.
答案:B 命题立意:本题主要考查了双曲线的定义、标准方程、几何性质以及基本量的计算等基础知识,考查了考生的推理论证能力以及运算求解能力.
解题思路:如图,由双曲线定义得,|BF1|-|BF2|=|AF2|-|AF1|=2a,因为ABF2是正三角形,所以|BF2|=|AF2|=|AB|,因此|AF1|=2a,|AF2|=4a,且F1AF2=120°,在F1AF2中,4c2=4a2+16a2+2×2a×4a×=28a2,所以e=,故选B.
9.已知直线l1:4x-3y+6=0和直线l2:x=-1,抛物线y2=4x上一动点P到直线l1和直线l2的距离之和的最小值是( )
A.2 B.3
C. D.
答案:A 解题思路:设抛物线y2=4x上一动点P到直线l1和直线l2的距离分别为d1,d2,根据抛物线的定义可知直线l2:x=-1恰为抛物线的准线,抛物线的焦点为F(1,0),则d2=|PF|,由数形结合可知d1+d2=d1+|PF|取得最小值时,即为点F到l1的距离,利用点到直线的距离公式得最小值为=2,故选A.
10.已知双曲线-=1(a>0,b>0),A,B是双曲线的两个顶点,P是双曲线上的一点,且与点B在双曲线的同一支上,P关于y轴的对称点是Q.若直线AP,BQ的斜率分别是k1,k2,且k1·k2=-,则双曲线的离心率是( )
A. B. C. D.
答案:C 命题立意:本题考查双曲线方程及其离心率的求解,考查化简及变形能力,难度中等.
解题思路:设A(0,-a),B(0,a),P(x1,y1),Q(-x1,y1),故k1k2=×=,由于点P在双曲线上,故有-=1,即x=b2=,故k1k2==-=-,故有e===,故选C.
二、填空题
11.已知抛物线y2=4x的焦点为F,过点P(2,0)的直线交抛物线于A(x1,y1)和B(x2,y2)两点,则(1)y1y2=________;(2)三角形ABF面积的最小值是________.
答案:(1)-8 (2)2 命题立意:本题主要考查直线与抛物线的位置关系,难度中等.
解题思路:设直线AB的方程为x-2=m(y-0),即x=my+2,联立得y2-4my-8=0.(1)由根与系数的关系知y1y2=-8.(2)三角形ABF的面积为S=|FP||y1-y2|=×1×=≥2.
知识拓展:将ABF分割后进行求解,能有效减少计算量.
12. B1,B2是椭圆短轴的两端点,O为椭圆中心,过左焦点F1作长轴的垂线交椭圆于P,若|F1B2|是|OF1|和|B1B2|的等比中项,则的值是________.
答案: 命题立意:本题考查椭圆的基本性质及等比中项的性质,难度中等.
解题思路:设椭圆方程为+=1(a>b>0),令x=-c,得y2=, |PF1|=. ==,又由|F1B2|2=|OF1|·|B1B2|,得a2=2bc. a4=4b2(a2-b2), (a2-2b2)2=0, a2=2b2, =.
13.已知抛物线C:y2=2px(p>0)的准线为l,过M(1,0)且斜率为的直线与l相交于点A,与C的一个交点为B.若=,则p=________.
答案:2 解题思路:过B作BE垂直于准线l于E,
=, M为AB的中点,
|BM|=|AB|,又斜率为,
BAE=30°, |BE|=|AB|,
|BM|=|BE|, M为抛物线的焦点,
p=2.
14.
如图,椭圆的中心在坐标原点O,顶点分别是A1,A2,B1,B2,焦点分别为F1,F2,延长B1F2与A2B2交于P点,若B1PA2为钝角,则此椭圆的离心率的取值范围为________.
答案: 解题思路:设椭圆的方程为+=1(a>b>0),B1PA2为钝角可转化为,所夹的角为钝角,则(a,-b)·(-c,-b)0, e>或e<,又0
15.在平面直角坐标系xOy中,已知双曲线C:-=1.设过点M(0,1)的直线l与双曲线C交于A,B两点,若=2,则直线l的斜率为________.
答案:± 命题立意:本题考查直线与双曲线的位置关系,难度中等.
解题思路:联立直线与双曲线,结合根与系数的关系及向量的坐标运算求解.由题意可知,直线l与双曲线的两支相交,故设直线l:y=kx+1,k,代入双曲线方程整理得(3-4k2)x2-8kx-16=0(*).设A(x1,y1),B(x2,y2),则由=2得x1=-2x2,在(*)中,利用根与系数的关系得x1+x2=,解得x2=-,y2=,代入双曲线方程整理得16k4-16k2+3=0,解得k2=,故直线l的斜率是±.
2017江苏高考数学太难考生痛哭 被葛军支配的恐惧
(1)先根据曲线y=f(x)在点(1,f(1))处的切线与直线x-y+1=0垂直关系,求切线的解析式,然后根据y=f(x)的切线方程求曲线y=f(x)的解析式,然后与原函数f(x)=alnx+bx进行对比,即可得a,b。
(2)根据所求的函数f(x)=alnx+bx的方程,代入f(x)<=(m-2)x-m/x,(x?[1,+00)),解不等式即可算出m的值。
2017高考状元事迹_2017高考状元事迹有哪些
每一年的高考过后,最受大家关注的就是数学考试。为什么这么说呢?我想大家都记得2003年的高考数学吧,也正是因为那一年江苏卷从此名震江湖。下面是我整理的2017年江苏高考数学难易程度,大家一起看下是否还是当年的水准。
2017年江苏高考数学难度
2003年,据说当年的高考数学江苏卷被人盗走,有泄题风险,于是特地用了当年的“替补卷”,这一张数学试卷的主出题人,是葛军老师,后来他也被被大家称为“高考数学帝”。同样的10年高考数学,江苏卷葛军再次参与出题。为什么把这两年一起讲呢?因为这两年的江苏卷,难度突然飙升,给考生们杀了个措手不及。
当年很多学生在考场都禁不住压力,边做题边哭,实在是太难了。有些考生更是走出考场就心理崩溃,哭得上气不接下气。这两年的全国平均分说法不一,大概在48分到68分左右,一套高考数学试卷,全国大部分考生竟然连一半的分数都没考到,可想而知难度如何。
后来几年的高考数学,虽然江苏卷依然难度比全国各省试卷都要大一些,但是没有再出现过这样的情况。不过今年确实情况堪忧,不少考生再次哭着走出考场,有学霸称考试太难,草稿纸差点不够,尽全力填补了试卷空白,不知结果如何。
老师闻此情况,特地把2017全国高考数学做了一个难度整理,认真评比之后认为,实际上今年的江苏卷和浙江卷难度不相上下,但是相比03年和10年情况还是要好很多。
高考数学答题注意事项1、抓住重点内容,注重能力培养
高中数学主体内容是支撑整个高考数学最重要的部分,也是进入大学必须掌握的内容,这些内容都是每年高考数学必考且重点考的。象关于函数(含三角函数)、平面向量、直线和圆锥曲线、线面关系、数列、概率、导数等,把它们作为复习中的重中之重来处理,要一个一个专题去落实,要通过对这些专题的复习向其他知识点辐射。
2、关心教育动态,注意题型变化
由于新增内容是当前社会生活和生产中应用比较广泛的内容,而与大学接轨内容则是进入大学后必须具备的知识,因此它们都是高考必考的内容,因此一定要把诸如概率与统计、导数及其应用、推理与证明、算法初步与框图的基本要求有目的的进行复习与训练。一定要用新的教学理念进行高三数学教学与复习,
3、细心审题、耐心答题,规范准确,减少失误
计算能力、逻辑推理能力是考试大纲中明确规定的两种培养的能力。可以说是学好数学的两种最基本能力,在数学试卷中的考查无处不在。并且在每年的阅卷中因为这两种能力不好而造成的失分占有相当的比例。所以我们在数学复习时,除抓好知识、题型、方法等方面的教学外,还应通过各种方式、机会提高和规范学生的运算能力和逻辑推理能力。
2017高考状元事迹一
谢畅者,不知何许人氏也,上谢下畅,不详其字,因其牛逼,人称?畅哥?。
畅哥就是个BUG,万能的畅哥永远稳居年级第一宝座,无人撼动,在畅哥面前,学霸这个词显得是多么的无力。
畅哥进校,毋庸置疑是第一,第一次月考后,畅哥所有科目除物理意外丢分外,均获年级第一佳绩。之后畅哥屡创神话,为大家塑造了学神的形象,被无数人奉为男神。
高一分科后,畅哥在近两个月没有学习文科的情况下,仍然文科突近德阳前三,力撼众人,当然总分是第一,这种小case对畅哥完全没有难度。
就在不久前,畅哥又创下了新的辉煌,总分突破710分大关,没错,畅哥在全真模拟期末统考的考试中,数学满分,语文130+,英语140+,理综近乎满分,是的,请和我一起叫他男神。
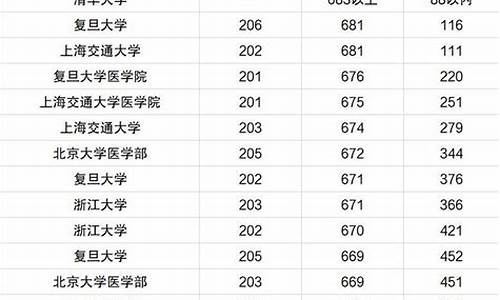
2017高考状元事迹二2016年四川高考文科状元:刘代蕾
绵阳中学文科考生刘代蕾以663分成为绵阳文科最高分。班主任何建波介绍,刘代蕾已进入清华大学领军计划,可降35分录取。该生文理科比较均衡,年级老师对她评价很高,学习很稳定,一直在前茅。品德表现都很优秀,好成绩是大家意料之中的。
2017高考状元事迹三满分750分,万妙然的成绩为681分!
文科生能考到这么高的分数,几乎是从来没有出现过的,甚至连北大清华的招生老师都表示说?简直不可思议?!
不过,成都外国语学校校长龚智发却说,她还考过不少次的700多分呢!
每一科成绩都在130分以上,用班主任的话来说,万妙然?没有弱点?。在网上,还流传着关于她的? 传说 ?,同学为了考好,会特地在考前去膜拜一下她。
22日晚9点过,华西都市报记者见到了万妙然,这个身高170的18岁女孩讲话爽朗,落落大方。对于此次的成绩,她说自己还是有一点点意外的,没想到自己考试的时候发挥得那么好。?以前考700多分,都是学校改卷子嘛,觉得可能跟高考的含金量不一样。?
总结 自己的?高分秘诀?,万妙然不断地重复,?重基础?不断训练?熟能生巧?。
学霸心得
注重?基础牢固?,有了基础,才会在考试的时候遇到陷阱不会?陷进去?。?做练习的目的不是看自己会不会,而是要练习熟练度,每一道题都要认真地对待。?
高考目标
选择哪个大学还未确定,专业比较倾向于建筑和经济金融方向。?对建筑感兴趣是因为我比较喜欢地理,就去了解了城乡规划,这个方向一般都在建筑学院里面。?
A
学霸秘诀
看哈利波特原版书学英语
?其实我喜欢每一个学科,他们都有很有意思的地方,但是如果硬从里面选的话,我最喜欢英语和地理。?万妙然的英语成绩为143分,只差7分就满分了。她也讲起了自己学英语的 方法 。
万妙然比较赞同成外注重学生英语?听说?能力的培养模式,每次英语课的前15分钟,会由值日生出一个题目,然后让学生做2分钟的小演讲。?这很大程度上锻炼了我们的表达能力,能够让我们在课堂上学到的东西及时的应用、消化。?
当然,在课外也需要知识的拓展和积累,万妙然的方法就是读英文原版小说,《哈利波特》、《指环王》、《纳尼亚传奇》、《霍比特人》等魔幻类小说是她的最爱。她是从高中的时候开始接触这一类的英文原著,?这一类的书籍,语言和内容都值得一读。?万妙然说。
除此之外,每天早上,万妙然总会抽15分钟左右的时间来做 英语阅读 理解和完形填空,?老师只能给你方法上的指导,做题的准确度,基础知识的掌握就必须靠不停的练习和实践。?
通过旅游学习地理知识
万妙然的妈妈缪辉辉是成都七中初中学校的地理老师,受妈妈熏陶,她对地理也非常感兴趣。?这可能跟我喜欢旅游是有关系的。?万妙然认为,旅游和地理其实是?双向验证?的过程,在旅游的过程中,可以把地理和实际生活联系起来,了解各种各样的地方和各种各样的事情。
几乎每年的假期,万妙然都会和妈妈出去旅游,全部都是自由行,大的方向由妈妈确定,行程细节则必须是她自己来做准备。国内,西北地区她去过敦煌看过飞天,去内蒙古看过胡杨林;西南地区,在九寨沟、四姑娘山、海螺沟也留下过足迹;东南地区,去过上海、苏州、杭州,感受城市里面的美。
?自然景观和人文景观的地方都有去,只要是没去过的地方,我都比较喜欢。?这不,高考成绩出来,志愿填报之后,母女俩就又要开始旅行了,这次她们的目的地是日本。
重基础 不断训练熟练度
仔细分析万妙然的分数,你会发现,她几乎每个学科的分数都非常高。万妙然说,她比较注重?基础牢固?,有了基础,才会在考试的时候遇到陷阱不会?陷进去?。?做练习的目的不是看自己会不会,而是要练习熟练度,每一道题都要认真地对待。?
地理老师万东说,万妙然自主学习能力很强,思维缜密,解答地理综合题尤为出众,几乎不会失分。而万妙然说,自己很在意基础题,她要求自己选择题和填空题一定不能错,宁愿放慢速度,也不让自己出错。
在练习所谓的?压轴题?的时候,要注重自己解题方法的积累,可以把题型分类,?达到一定的练习量之后,就能够归纳出几种分类了。?万妙然说,老师规定她每周在完成作业之后,要找一定的 拓展训练 题目训练,这样才能保持?手感?。
?她在高一、高二是学习委员,高三是班长,在班上很有凝聚力,还积极帮助其他同学答疑解惑。?万东说道。帮同学解答疑问,在万妙然看来,这其实是一个双赢的过程。?在解答问题的过程中,也能看到自己的缺失。?
B
个人成长
网传曾遭同学考前膜拜
?不要把我当考神?
3年前,万妙然以中考675分的成绩,从七中初中升入成外,据说,当时这个成绩在全成都市的排名中也是非常靠前的。
进入高中,万妙然一直保持着良好的学习习惯和行为习惯。每天早上6点40左右起床,吃完早饭后,有固定时间做英语习题,晚饭后再用固定的时间练习语文基础知识,晚上则要加班到12点过才会睡觉。?有些知识是需要一遍一遍的来,才能确保不会出错。?
而此次的高分,在万妙然看来,是跟自己长期的积累分不开的,要在考试中发现自己的问题,以各种方式不断地完善自己。?我心态也是很好的,做题的时候比较专注。?
万妙然成绩出来之后,在网络上流传着她的?传奇经历?,有同学为了考试顺利,每到考试前就去?膜拜?一下她。对此,万妙然笑着说没有那么夸张。?我不希望别人把我当做考神,大家都是需要互 相学 习的。?
她喜欢建筑和经济
获清华55分加分录取资格
?万妙然是一个很有想法、敢于质疑问难的小姑娘,她常常会在课堂上就一个问题提出自己独到的见解,不盲从。正因为这点,学习对她来说不是任务,反倒是一种乐趣。?班主任唐有益评价说。
除此之外,唐有益说,万妙然还喜欢书法,写的 日记 、游记也赏心悦目。同时也是一个很有号召力的娃娃,高一暑假,班上准备集体出一个叫做《前朝》的文集,她还主动承担起编委的工作,帮同学看稿子,提意见。
据介绍,万妙然此前参加了清华大学的百年领军计划的自主招生项目,获得了加55分的优惠政策。而对于选择哪个大学,万妙然说还未确定,但是对于专业,她比较倾向于建筑和经济金融方向。?对建筑感兴趣是因为我比较喜欢地理,就去了解了城乡规划,这个方向一般都在建筑学院里面。?
她的班主任/
教出4个省第一
成都市劳模、四川省特级教师、语文老师唐有益;四川省优秀教师、数学老师于开选;成都市优秀班主任、地理老师万东?成外高2015届年级主任杨登文告诉记者,这个似曾相识的教师团队,不仅带出了今年的省文科第一名,也培养出2012年省文科第一名周小琪、理科第一名高蕊馨。班主任唐有益被称为?成外师尊?,他还带出了2004年理科第一名王舸。?整个教师团队非常团结,正是因为他们善于打团体仗,才能培养出这么有凝聚力的班级。?
离高考还有三个月的时候,66岁的班主任唐有益坚持每天陪学生一起上晚自习到10点半。三个半小时的自习时间,科任老师在前面讲,唐有益有时坐在最后一排听,有时绕着教室一圈圈走,几乎不答疑,只是?作为一种陪伴,与学生同行?。去年年底,在班上同学准备保送考试之前,?万姐?万妙然为了给同学打气,一大早就在黑板上写上大大的几个字:?祝保送的小伙伴们心想事成、梦想成真!?令班上每个人心中都暖意洋洋。
她的同学/
全班26人被保送
59人的班级,7名学生 出国 ,其中一人考进哈佛;26名学生被保送到北大、清华等名校;参加高考的26人中,诞生了今年四川省文科第一名万妙然。这就是人称?学霸班级?的成都外国语学校2015届13班。
22日晚,2015年高考成绩陆续出炉,成外高三分管副校长路跃陆续收到来自高2015届13班的学生的报信:袁维寒660分,肖楷654分,赖雨琦639分,王紫剑636分?而零诊、三诊成绩均上700分的万妙然,以681分的高分毫无悬念拿下四川省高考文科第一名。
?这个班并非万妙然一枝独秀,?路跃告诉记者,全班59人中,7名学生出国,其中张潇月考进哈佛大学;26名学生被保送到北大、清华、复旦、浙大等名校;参加高考的26名学生中,除了万妙然,也有不少上630分的学霸们。
她的父母/
注重开发女儿的?热爱?
?从小,我们就非常注重她良好性格和品格的培养。?爸爸万新说,在女儿还很小的时候,他就给女儿听磁带、听 故事 、看书,搭积木,锻炼女儿的语言、行为和思考能力。他一直持续的比较好的习惯就是,从女儿两岁多一直到上小学的时候,他坚持每晚都给女儿讲故事,婴幼儿画报、小故事大智慧,甚至是现场编故事。?其实到了高三,我爸还每天给我发一两个笑话过来。?万妙然说。
而妈妈的 教育 则比较注重开发女儿的?热爱?,她希望女儿能热爱生活、热爱学习,?因为只有热爱才能坚持下去?。有着22年教学历史的缪辉辉是七中初中?云教育实验班?的班主任,平时假期,她总是带着女儿去发掘好吃的好玩的,只要有长时间的假期,两人就会结伴出去旅游,而且是自由行。?热爱生活的万妙然喜欢听爱尔兰和北欧的民谣歌曲,高考前的一天,她还在家里听歌,乱唱。?