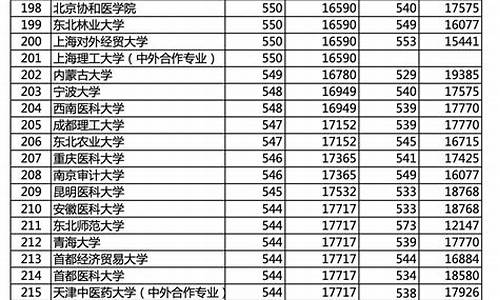
您现在的位置是: 首页 > 教育改革 教育改革
2014年高考数列_2014高考数列题
tamoadmin 2024-05-29 人已围观
简介1.高三数学数列测试题及答案2.为什么2014年湖南高考数学这么难3.2014年安徽理科数学21题的解答方法是什么啊?还是很难的,难怪是高考压轴题啊,毫无思路这个题主要考查等差数列和等比数列的性质.做这种题要求我们对等差数列和等比数列的通项公式,求和公式熟练记忆.只有这样这种题才能解答答案这个题不是很难,感觉你应该能看明白,希望你采纳,谢谢,么么哒等差数列{an}满足:a1=2,且a1,a2,a5
1.高三数学数列测试题及答案
2.为什么2014年湖南高考数学这么难
3.2014年安徽理科数学21题的解答方法是什么啊?还是很难的,难怪是高考压轴题啊,毫无思路
这个题主要考查等差数列和等比数列的性质.做这种题要求我们对等差数列和等比数列的通项公式,求和公式熟练记忆.只有这样这种题才能解答答案这个题不是很难,感觉你应该能看明白,希望你采纳,谢谢,么么哒
等差数列{an}满足:a1=2,且a1,a2,a5成等比数列.
(I)求{an}的通项公式;
(II)记Sn为数列{an}的前n项和,是否存在正整数n,使得Sn>60n+800?若存在,求n的最小值;
高三数学数列测试题及答案
人生需要反思,总结才能远航,回首往夕,收获的是经验和提高。下面就是我整理的数列解题方法技巧总结,一起来看一下吧。
学生们在高中的数学学习过程中如果能够充分掌握高中数学数列试题的解题方法和技巧,这对于在大学期间学习数学会有很大的帮助。在最近几年的数学高考中,数列知识点的考查已经成为高考出题人比较看重的一项考点,甚至有一部分拔高题也都和数列有着直接的关系。可是在高中数学的学习阶段,很多的学生对于高中数学数列试题的解题方法和技巧还非常欠缺,对有一些问题和内容并没有得到充分的理解和吸收,往往在解题过程中,出现这样那样的问题。所以,探索和研究不同类型数列的解题方法和技巧,能够帮助学生更好地学好高中的数学。
高中数学数列试题教学中的解题思路与技巧
1.对数列概念的考查
在高中数列试题中,有一些试题可以直接通过带入已学的通项公式或求和公式,就可以得到答案,面对这一种类型的试题,没有什么技巧而言,我们只需熟练掌握相关的数列公式即可。
例如:在各项都为正数的等比数列{b}中,首项b1=3,b1+b2+b3=21,那么b3+b4+b5等于多少?
解析:(1)本道试题主要是对正项数列的概念以及等比数列的通项公式和求和公式知识点的考查,考查学生对数列基础知识和基本运算的掌握能力。
(2)本试题要求学生要熟练掌握老师在课堂上所教的通项公式和求和公式。
(3)首先让我们来求公比,很明显q不等1,那么我们可以根据我们所学过的等比数列前项和公式,列出关于公比的方程,即3(1-q3)/(1-q)=21。
对于这个方程,我们首先要选择其运算的方式,要求学生平时的练习过程中,要让学生能够熟练地将高次方程转化为低次方程进行运算。
2.对数列性质的考察
有些数列的试题中,经常会变换一些说法来考查学生对数列的基本性质的`理解和掌握能力。
例如:己知等差数列{xn},其中xl+x7=27,求x2+x3+x5+x6等于多少?
解析:我们在课堂上学习过这样的公式:等差数列和等比数列中m+n=p+q,我们可以充分利用这一特性来解此题,即:
xl+x7= x2+x6= x3+x5=27,
因此,x2+x3+x5+x6=(x2+x6)+(x3+x5)=27+27=54
这种类型的数列试题要求教师在课堂教学中,对数列的性质竟详细讲解,仔细推导。使得学生能够真正的理解数列性质的来源。
3.对求通项公式的考察
①利用等差、等比数列的通项公式,求通项公式
②利用关系an={S1,n=1;Sn-Sn-1,n≥2}求通项公式
③利用叠加、叠乘法求通项公式
④利用数学归纳法求通项公式
⑤利用构造法求通项公式.
4.求前n项和的一些方法
在最近几年的数学高考试题中,数列通项公式和数列求和这两个知识点是每年必考的,因此,在高中数学数列的课堂教学中,教师要对数列求和通项公式这方面的知识点进行细致重点的讲解。数列求和的主要解题方法有错位相减法、分组求和法与合并求和法,下面对三种数列求和的解题方法进行详细说明。
(1)错位相减法
错位相减法主要应用于等比数列的求和中,在最近几年的高考试题当中,以此方法来求解数列求和的试题经常会有所体现。这一类型的试题解题方法主要是运用于诸如{等差数列·等比数列}数列前n项和的求和中。
例如:已知{xn}是等差数列,其前n项和是Sn,{yn}是等比数列,且x1=y1=2, x4+y4=27, S4-y4=10,求(1)求数列{xn}与{yn}的通项公式;(2)Tn= xny1+xn-1y2+…+x1yn,n∈N*证明Tn+12=-2xn+10yn,n∈N*
解析:(1)xn=3n-1,yn=2n;
(2)Tn= 2xn+22xn-1+23xn-2+…+2nx1,
2Tn= 22xn+23xn-1+…+2nx2+2n+1x1
计算得,Tn=-2(3n-1)+3×22+3×23+…+3×2n+2n+1=12(1-2n+1)/(1-2+2n+2-6n+2)=10×2n-6n-10
-2an+10bn-12=-2(3n-1)+10×2n-12=10×2n-6n-10
所以,Tn+12=-2xn+10yn,n∈N*
错位相减法主要应用于形如an=bncn,即等差数列·等比数列,这样的数列求和试题运算中,解此类题的技巧是:首先分别列出等差数列和等比数列的前n的和,即Sn,然后再分别将Sn的两侧同时乘以等比数列的公比q,得出qSn;最后错一位,再将两边的式子进行相减就可以了。
(2)分组法求和
在高中数列的试题当中,往往会遇到一部分没有规律的数列试题,它们初看上去既不属于等差数列也不属于等比数列,但是如果将此类型的数列进行拆分,就可以得到我们所了解的等差数列和等比数列,遇到此类型的数列试题,我们就可以通过分组法求和的方法进行解题,首先将数列进行拆分,通过得到的等差数列和等比数列进行运算,最后将其结合在一起得出试题的答案。
(3)合并法求和
在高考数列的试题中,往往会遇到一些非常特殊的题型,它们初看上去没有规律可循,但是通过合并和拆分,就可以找出它们的特殊性质。这就要求我们教师平时要锻炼学生对数列的合并能力,通过合并找出规律,最终成功地解决这类特殊数列的求和问题。
结束语
数列知识是各种数学知识的连接点,在数学考试中,往往是基于数列知识为基础,对学生的综合数学知识进行考查。在高中数列学习过程中,首先要做好数列基本概念和基本性质的掌握,否则任何解题技巧都无济于事。
为什么2014年湖南高考数学这么难
一、选择题:本大题共12小题,每小题5分,共60分.
1.在等差数列{an}中,若a1+a2+a12+a13=24,则a7为( )
A.6 B.7 C.8 D.9
解析:∵a1+a2+a12+a13=4a7=24,∴a7=6.
答案:A
2.若等差数列{an}的前n项和为Sn,且满足S33-S22=1,则数列{an}的公差是( )
A.12 B.1 C.2 D.3
解析:由Sn=na1+n(n-1)2d,得S3=3a1+3d,S2=2a1+d,代入S33-S22=1,得d=2,故选C.
答案:C
3.已知数列a1=1,a2=5,an+2=an+1-an(n∈N*),则a2 011等于( )
A.1 B.-4 C.4 D.5
解析:由已知,得a1=1,a2=5,a3=4,a4=-1,a5=-5,a6=-4,a7=1,a8=5,…
故{an}是以6为周期的数列,
∴a2 011=a6×335+1=a1=1.
答案:A
4.设{an}是等差数列,Sn是其前n项和,且S5<S6,S6=S7>S8,则下列结论错误的是( )
A.d<0 B.a7=0
C.S9>S5 D.S6与S7均为Sn的最大值
解析:∵S5<S6,∴a6>0.S6=S7,∴a7=0.
又S7>S8,∴a8<0.
假设S9>S5,则a6+a7+a8+a9>0,即2(a7+a8)>0.
∵a7=0,a8<0,∴a7+a8<0.假设不成立,故S9<S5.∴C错误.
答案:C
5.设数列{an}是等比数列,其前n项和为Sn,若S3=3a3,则公比q的值为( )
A.-12 B.12
C.1或-12 D.-2或12[
解析:设首项为a1,公比为q,
则当q=1时,S3=3a1=3a3,适合题意.
当q≠1时,a1(1-q3)1-q=3a1q2,
∴1-q3=3q2-3q3,即1+q+q2=3q2,2q2-q-1=0,
解得q=1(舍去),或q=-12.
综上,q=1,或q=-12.
答案:C
6.若数列{an}的通项公式an=5 252n-2-425n-1,数列{an}的最大项为第x项,最小项为第y项,则x+y等于( )
A.3 B.4 C.5 D.6
解析:an=5252n-2-425n-1=525n-1-252-45,
∴n=2时,an最小;n=1时,an最大.
此时x=1,y=2,∴x+y=3.
答案:A
7.数列{an}中,a1 =15,3an+1= 3an-2(n∈N *),则该数列中相邻两项的乘积是负数的是( )
A.a21a22 B.a22a23 C.a23a24 D.a24a25
解析:∵3an+1=3an-2,
∴an+1-an=-23,即公差d=-23.
∴an=a1+(n-1)d=15-23(n-1).
令an>0,即15-23(n-1)>0,解得n<23.5.
又n∈N*,∴n≤23,∴a23>0,而a24<0,∴a23a24<0.
答案:C
8.某工厂去年产值为a,计划今后5年内每年比上年产值增加10%,则从今年起到第5年,这个厂的总产值为( )
A.1.14a B.1.15a
C.11×(1.15-1)a D.10×(1.16-1)a
解析:由已知,得每年产值构成等比数列a1=a,w
an=a(1+10%)n-1(1≤n≤6).
∴总产值为S6-a1=11×(1.15-1)a.
答案:C
9.已知正数组成的等差数列{an}的前20项的和为100,那么a7a14的最大值为( )
A.25 B.50 C.1 00 D.不存在
解析:由S20=100,得a1+a20=10. ∴a7+a14=10.
又a7>0,a14>0,∴a7a14≤a7+a1422=25.
答案:A
10.设数列{an}是首项为m,公比为q(q≠0)的等比数列,Sn是它的前n项和,对任意的n∈N*,点an,S2nSn( )
A.在直线mx+qy-q=0上
B.在直线qx-my+m=0上
C.在直线qx+my-q=0上
D.不一定在一条直线上
解析:an=mqn-1=x, ①S2nSn=m(1-q2n)1-qm(1-qn)1-q=1+qn=y, ②
由②得qn=y-1,代入①得x=mq(y-1), 即qx-my+m=0.
答案:B
11.将以2为首项的偶数数列,按下列分组:(2),(4,6),(8,10,12),…,第n组有n个数,则第n组的首项为( )
A.n2-n B.n2+n+2
C.n2+n D.n2-n+2
解析:因为前n-1组占用了数列2,4,6,…的前1+2+3+…+(n-1)=(n-1)n2项,所以第n组的首项为数列2,4,6,…的第(n-1)n2+1项,等于2+(n-1)n2+1-12=n2-n+2.
答案:D
12.设m∈N*,log2m的整数部分用F(m)表示,则F(1)+F(2)+…+F(1 024)的值是( )
A.8 204 B.8 192
C.9 218 D.以上都不对
解析:依题意,F(1)=0,
F(2)=F(3)=1,有2 个
F(4)=F(5)=F(6)=F(7)=2,有22个.
F(8)=…=F(15)=3,有23个.
F(16)=…=F(31)=4,有24个.
…
F(512)=…=F(1 023)=9,有29个.
F(1 024)=10,有1个.
故F(1)+F(2)+…+F(1 024)=0+1×2+2×22+3×23+…+9×29+10.
令T=1×2+2×22+3×23+…+9×29,①
则2T=1×22+2×23+…+8×29+9×210.②
①-②,得-T=2+22+23+…+29-9×210 =
2(1-29)1-2-9×210=210-2-9×210=-8×210-2,
∴T=8×210+2=8 194, m]
∴F(1)+F(2)+…+F(1 024)=8 194+10=8 204.
答案:A
第Ⅱ卷 (非选择 共90分)
二、填空题:本大题共4个小题,每小题5分 ,共20分.
13.若数列{an} 满足关系a1=2,an+1=3an+2,该数 列的通项公式为__________.
解析:∵an+1=3an+2两边加上1得,an+1+1=3(an+1),
∴{an+1}是以a1+1=3为首项,以3为公比的等比数列,
∴an+1=33n-1=3n,∴an=3n-1.
答案:an=3n-1
14.已知公差不为零的等差数列{an}中,M=anan+3,N=an+1an+2,则M与N的大小关系是__________.
解析:设{an}的公差为d,则d≠0.
M-N=an(an+3d)-[(an+d)(an+2d)]
=an2+3dan-an2-3dan-2d2=-2d2<0,∴M<N.
答案:M<N
15.在数列{an}中,a1=6,且对任意大于1的正整数n,点(an,an-1)在直线x-y=6上,则数列{ann3(n+1)}的前n项和Sn=__________.
解析:∵点(an,an-1)在直线x-y=6上,
∴an-an-1=6,即数列{an}为等差数列.
∴an=a1+6(n-1)=6+6(n-1)=6n,
∴an=6n2.
∴ann3(n+1)=6n2n3(n+1)=6n(n+1)=61n-1n+1
∴Sn=61-12+12-13+…+1n-1n+1.=61-1n+1=6nn+1.
答案:6nn+1
16.观察下表:
1
2 3 4
3 4 5 6 7
4 5 6 7 8 9 10
…
则第__________行的各数之和等于2 0092.
解析:设第n行的各数之和等于2 0092,
则此行是一个首项a1=n,项数为2n-1,公差为1的等差数列.
故S=n×(2n-1)+(2n-1)(2n-2)2=2 0092, 解得n=1 005.
答案:1 005
三、解答题:本大题共6小题,共70分.
17.(10分)已知数列{an}中,a1=12,an+1=12an+1(n∈N*),令bn=an-2.
(1)求证:{bn}是等比数列,并求bn;
(2)求通项an并求{an}的前n项和Sn.
解析:(1)∵bn+1bn=an+1-2an-2=12an+1-2an-2=12an-1an-2=12,
∴{bn}是等比数列.
∵b1=a1-2=-32,
∴bn=b1qn-1=-32×12n-1=-32n.
(2)an=bn+2=-32n+2,
Sn=a1+a2+…+an
=-32+2+-322+2+-323+2+…+-32n+2
=-3×12+122+…+12n+2n=-3×12×1-12n1-12+2n=32n+2n-3.
18.(12分)若数列{an}的前n项和Sn=2n.
(1)求{an}的通项公式;
(2)若数列{bn}满足b1=-1,bn+1=bn+(2n-1),且cn=anbnn,求数列{cn}的通项公式及其前n项和Tn.
解析:(1)由题意Sn=2n,
得Sn-1=2n-1(n≥2),
两式相减,得an=2n-2n-1=2n-1(n≥2).
当n=1时,21-1=1≠S1=a1=2.
∴an=2 (n=1),2n-1 (n≥2).
(2)∵bn+1=bn+(2n-1),
∴b2-b1=1,
b3-b2=3,
b4-b3=5,
…
bn-bn-1=2n-3.
以上各式相加,得
bn-b1=1+3+5+…+(2n-3)
=(n-1)(1+2n-3)2=(n-1)2.
∵b1=-1,∴bn=n2-2n,
∴cn=-2 (n=1),(n-2)×2n-1 (n≥2),
∴Tn=-2+0×21+1×22+2×23+…+(n-2)×2n-1,
∴2Tn=-4+0×22+1×23+2×24+…+(n-2)×2n.
∴-Tn=2+22+23+…+2n-1-(n-2)×2n
=2(1-2n-1)1-2-(n-2)×2n
=2n-2-(n-2)×2n
=-2-(n-3)×2n.
∴Tn=2+(n-3)×2n.
19.(12分)已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.
(1)求数列{an}的通项公式;
(2)若从数列{an}中依次取出第2项,第4项,第8项,…,第2n项,…,按原来顺序组成一个新数列{bn},记该数列的前n项和为Tn,求Tn的表达式.
解析:(1)依题意,得
3a1+3×22d+5a1+5×42d=50,(a1+3d)2=a1(a1+12d),解得a1=3,d=2.
∴an=a1+(n-1)d=3+2(n-1)=2n+1,
即an=2n+1.
(2)由已知,得bn=a2n=2×2n+1=2n+1+1,
∴Tn=b1+b2+…+bn
=(22+1)+(23+1)+…+(2n+1+1)
=4(1-2n)1-2+n=2n+2-4+n.
20.(12分)设数列{an}的前n项和为Sn,且ban-2n=(b-1)Sn.
(1)证明:当b=2时,{an-n2n-1}是等比数列;
(2)求通项an. 新 课 标 第 一 网
解析:由题意知,a1=2,且ban-2n=(b-1)Sn,
ban+1-2n+1=(b-1)Sn+1,
两式相减,得b(an+1-an)-2n=(b-1)an+1,
即an+1=ban+2n.①
(1)当b=2时,由①知,an+1=2an+2n.
于是an+1-(n+1)2n=2an+2n-(n+1)2n
=2an-n2n-1.
又a1- 120=1≠0,
∴{an-n2n-1}是首项为1,公比为2的等比数列.
(2)当b=2时,
由(1)知,an-n2n-1=2n-1,即an=(n+1)2n-1
当b≠2时,由①得
an +1-12-b2n+1=ban+2n-12-b2n+1=ban-b2-b2n
=ban-12-b2n,
因此an+1-12-b2n+1=ban-12-b2n=2(1-b)2-bbn.
得an=2, n=1,12-b[2n+(2-2b)bn-1], n≥2.
21.(12分)某地在抗洪抢险中接到预报,24小时后又一个超最高水位的洪峰到达,为保证万无一失,抗洪指挥部决定在24小时内另筑起一道堤作为第二道防线.经计算,如果有 20辆大型翻斗车同时作业25小时,可以筑起第二道防线,但是除了现有的一辆车可以立即投入作业外,其余车辆需从各处紧急抽调,每隔20分钟就有一辆车到达并投入.问指挥部至少还需组织多少辆车这样陆续,才能保证24小时内完成第二道防线,请说明理由.
解析:设从现有这辆车投入工作算起,各车的工作时间依次组成数列{an},则an-an-1=-13.
所以各车的工作时间构成首项为24,公差为-13的等差数列,由题知,24小时内最多可抽调72辆车.
设还需组织(n-1)辆车,则
a1+a2+…+an=24n+n(n-1)2×-13≥20×25.
所以n2-145n+3 000≤0,
解得25≤n≤120,且n≤73.
所以nmin=25,n-1=24.
故至少还需组织24辆车陆续工作,才能保证在24小时内完成第二道防线.
22.(12分)已知点集L={(x,y)y=mn},其中m=(2x-2b,1),n=(1,1+2b),点列Pn(an,bn)在点集L中,P1为L的轨迹与y轴的交点,已知数列{an}为等差数列,且公差为1,n∈N*.
(1)求数列{an},{bn}的通项公式;
(3)设cn=5nanPnPn+1(n≥2),求c2+c3+c4+…+cn的值.
解析:(1)由y=mn,m=(2x-2b,1),n=(1,1+2b),
得y=2x+1,即L:y=2x+1.
∵P1为L的轨迹与y轴的交点,
∴P1(0,1),则a1=0,b1=1.
∵数列{an}为等差数列,且公差为1,
∴an=n-1(n∈N*) .
代入y=2x+1,得bn=2n-1(n∈N*).
(2)∵Pn(n-1,2n-1),∴Pn+1(n,2n+1).
=5n2-n-1=5n-1102-2120.
∵n∈N*,
(3)当n≥2时,Pn(n-1,2n-1),
∴c2+c3+…+cn
=1-12+12-13+…+1n-1-1n=1-1n.
2014年安徽理科数学21题的解答方法是什么啊?还是很难的,难怪是高考压轴题啊,毫无思路
我觉得比去年难一些关键就是在题目不管是顺序还是比重都有所创新,小题不难,难在大题啊,考完后仔细想了一想其实也没有考的时候的那么难,我们同学都是这么反应的,所以还是有很多题的分是我们应该拿到的,这些会的题堆积起来,就可以考一个非常理想的分数啦。
本题是一道压轴题,考查的知识众多,涉及到函数,数列,不等式,利用的方法有分析法与综合法等,综合性很强,难度较大.答案看这里构造函数,等价转化是关键
设实数c>0,整数p>1,n∈N*
证明:当x>-1且x不等于 0时,(1+x)^p>1+px
数列{an}满足a1>c^(1/p),an+1=(p-1)an/p+ c*[an^(1-p)]/p。证明an>an+1>c^(1/p)