高考立体几何题目_高考立体几何试题分析

1.同为高考数学题，金字塔和天坛哪个考的更难？

2.立体几何高考题

⑴

∵M是等腰△SBC的中点

∴SM⊥BC

∵平面SBC⊥底面ABCD

∴SM⊥底面ABCD

M点是矩形一边的中点

且两边关系是1：2

∴容易证明 MA⊥MD

∵AM⊥SM AM⊥MD

∴AM⊥平面SMD（如果一条直线垂直于一个

平面的两条相交直线，那么这条直线垂直于

这样平面）

∴平面SMK⊥平面SAM（如果一个平面经过另一个

平面的垂线，那么这两个平面互相垂直）

⑵

同为高考数学题，金字塔和天坛哪个考的更难？

1．[2004年全国高考(山东山西河南河北江西安徽卷)理科数学第10题，文科数学第10题]

已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H.设四面体EFGH的表面积为T，则等于（）

A．B．C．D．

2．[2004年全国高考(山东山西河南河北江西安徽卷)理科数学第16题，文科数学第16题]

已知a、b为不垂直的异面直线，是一个平面，则a、b在上的射影有可能是.

①两条平行直线②两条互相垂直的直线

③同一条直线④一条直线及其外一点

在一面结论中，正确结论的编号是（写出所有正确结论的编号）.

3．[2004年全国高考(四川云南吉林黑龙江)文科数学第6题]

正四棱锥的侧棱长与底面边长都是1，则侧棱与底面所成的角为（）

A．75°B．60°C．45°D．30°

4．[2004年全国高考(四川云南吉林黑龙江)理科数学第7题，文科数学第10题]

已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离均为，则

球心O到平面ABC的距离为（）

A．B．C．D．

5．[2004年全国高考(四川云南吉林黑龙江)理科数学第16题，文科数学第16题]

下面是关于四棱柱的四个命题：

①若有两个侧面垂直于底面，则该四棱柱为直四棱柱

②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱

③若四个侧面两两全等，则该四棱柱为直四棱柱

④若四棱柱的四条对角线两两相等，则该四棱柱为直四棱柱

其中，真命题的编号是（写出所有正确结论的编号）.

6．[2004年全国高考(陕西广西海南西藏内蒙古)理科数学第9题，文科数学第10题]

正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为（）

A．B．C．D．

7．[2004年全国高考(陕西广西海南西藏内蒙古)理科数学第13题，文科数学第14题]

用平面截半径为的球，如果球心到平面的距离为，那么截得小圆的面积与球的表面积的比值为.

8．[2004年全国高考(甘肃贵州青海宁夏新疆)文科数学第3题]

正三棱柱侧面的一条对角线长为2，且与底面成45°角，则此三棱柱的体积为（）

A．B．C．D．

9．[2004年全国高考(甘肃贵州青海宁夏新疆)理科数学第7题]

对于直线m、n和平面，下面命题中的真命题是（）

A．如果、n是异面直线，那么

B．如果、n是异面直线，那么相交

C．如果、n共面，那么

D．如果、n共面，那么

10．[2004年全国高考(甘肃贵州青海宁夏新疆)文科数学第11题]

已知球的表面积为20，球面上有A、B、C三点.如果AB=AC=BC=2，则球心到平

面ABC的距离为（）

A．1B．C．D．2

11．[2004年全国高考(甘肃贵州青海宁夏新疆)理科数学第10题]

已知球的表面积为20π，球面上有A、B、C三点.如果AB=AC=2，BC=，则球心

到平面ABC的距离为（）

A．1B．C．D．2

12．（2004年北京高考·理工第3题，文史第3题）

设m、n是两条不同的直线，是三个不同的平面，给出下列四个命题：

①若，，则

②若，，，则

③若，，则

④若，，则

其中正确命题的序号是

A. ①和②B. ②和③C. ③和④D. ①和④

13．（2004年北京高考·理工第4题，文史第6题）

如图，在正方体中，P是侧面内一动点，若P到直线BC与直线的距离相等，则动点P的轨迹所在的曲线是

A. 直线B. 圆C. 双曲线D. 抛物线

14．（2004年北京高考·理工第11题，文史第12题）

某地球仪上北纬纬线的长度为，该地球仪的半径是__________cm，

表面积是______________cm2

15．[2004年全国高考(山东山西河南河北江西安徽卷)理科数学第20题，文科数学第21题，满分12分]

如图，已知四棱锥 P—ABCD，PB⊥AD，侧面PAD为边长等于2的正三角形，底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.

（I）求点P到平面ABCD的距离；

（II）求面APB与面CPB所成二面角的大小.

16．[2004年全国高考(四川云南吉林黑龙江)理科数学第20题，文科数学第20题，满分12分]

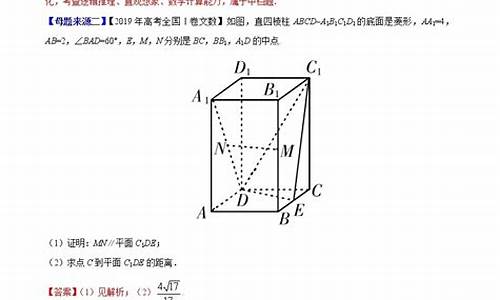
如图，直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=1，CB=，侧棱AA1=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M.

（Ⅰ）求证CD⊥平面BDM；

（Ⅱ）求面B1BD与面CBD所成二面角的大小.

17．[2004年全国高考(陕西广西海南西藏内蒙古)理科数学第20题，文科数学第21题，满分12分]

三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3，

（1）求证：AB ⊥ BC；

（2，理科）设AB=BC=，求AC与平面PBC所成角的大小.

(2，文科) 如果AB=BC=，求侧面PBC与侧面PAC所成二面角的大小.

18．[2004年全国高考(甘肃贵州青海宁夏新疆)理科数学第20题，文科数学第21题，本小题满分12分]

如图，四棱锥P—ABCD中，底面ABCD 为矩形，AB=8，AD=4，侧面PAD为等边三角形，并且与底面所成二面角为60°.

（Ⅰ）求四棱锥P—ABCD的体积；

（Ⅱ）证明PA⊥BD.

19．（2004年北京高考·文史第16题，本小题满分14分）

如图，在正三棱柱中，AB＝2，，由顶点B沿棱柱侧面经过棱到顶点的最短路线与的交点记为M，求：

（I）三棱柱的侧面展开图的对角线长

（II）该最短路线的长及的值

（III）平面与平面ABC所成二面角（锐角）的大小

20．（2004年北京高考·理工第16题，本小题满分14分）

如图，在正三棱柱中，AB＝3，，M为的中点，P是BC上一点，且由P沿棱柱侧面经过棱到M的最短路线长为，设这条最短路线与的交点为N，求：

（I）该三棱柱的侧面展开图的对角线长

（II）PC和NC的长

（III）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）

参考答案

1．A2．①②④3．C4．B5．②④6．C7．8．A9．C

10．A11．A12．A13．D14．

15．[2004年全国高考(山东山西河南河北江西安徽卷)理科数学第20题，文科数学第21题]

本小题主要考查棱锥，二面角和线面关系等基本知识，同时考查空间想象能力和推理、运算能力.满分12分.

（I）解：如图，作PO⊥平面ABCD，垂足为点O.连结OB、OA、OD、OB与AD交于点E，连结PE.

∵AD⊥PB，∴AD⊥OB，

∵PA=PD，∴OA=OD，

于是OB平分AD，点E为AD的中点，所以PE⊥AD.

由此知∠PEB为面PAD与面ABCD所成二面角的平面角，

∴∠PEB=120°，∠PEO=60°

由已知可求得PE=

∴PO=PE·sin60°=，

即点P到平面ABCD的距离为.

（II）解法一：如图建立直角坐标系，其中O为坐标原点，x轴平行于DA.

.连结AG.

又知由此得到：

所以

等于所求二面角的平面角，

于是

所以所求二面角的大小为.

解法二：如图，取PB的中点G，PC的中点F，连结EG、AG、GF，则AG⊥PB，FG//BC，FG=BC.

∵AD⊥PB，∴BC⊥PB，FG⊥PB，

∴∠AGF是所求二面角的平面角.

∵AD⊥面POB，∴AD⊥EG.

又∵PE=BE，∴EG⊥PB，且∠PEG=60°.

在Rt△PEG中，EG=PE·cos60°=.

在Rt△PEG中，EG=AD=1.

于是tan∠GAE==,

又∠AGF=π－∠GAE.

所以所求二面角的大小为π－arctan.

16．[2004年全国高考(四川云南吉林黑龙江)理科数学第20题，文科数学第20题]

本小题主要考查线面关系和直棱柱等基础知识，同时考查空间想象能力和推理运算能力.

满分12分.

解法一：（Ⅰ）如图，连结CA1、AC1、CM，则CA1=

∵CB=CA1=，∴△CBA1为等腰三角形，

又知D为其底边A1B的中点，

∴CD⊥A1B.∵A1C1=1，C1B1=，∴A1B1=

又BB1=1，A1B=2. ∵△A1CB为直角三角形，D为A1B的中点，

∴CD=A1B=1，CD=CC1，又DM=AC1=，DM=C1M.

∴△CDM≌△CC1M，∠CDM=∠CC1M=90°，即CD⊥DM.

因为A1B、DM为平在BDM内两条相交直线，所以CD⊥平面BDM.

（Ⅱ）设F、G分别为BC、BD的中点，连结B1G、FG、B1F，则FG//CD，FG=CD.

∴FG=，FG⊥BD.

由侧面矩形BB1A1A的对角线的交点为D知BD=B1D=A1B=1，

所以△BB1D是边长为1的正三角形.

于是B1G⊥BD，B1G=∴∠B1GF是所求二面角的平面角，

又 B1F2=B1B2+BF2=1+（=，

∴

即所求二面角的大小为

解法二：如图，以C为原点建立坐标系.

（Ⅰ）B（，0，0），B1（，1，0），A1（0，1，1），

D（，M（，1，0），

则∴CD⊥A1B，CD⊥DM.

因为A1B、DM为平面BDM内两条相交直线，所以CD⊥平面BDM.

（Ⅱ）设BD中点为G，连结B1G，则

G（），、、），

所以所求的二面角等于

17．[2004年全国高考(陕西广西海南西藏内蒙古)理科数学第20题，文科数学第21题]

本小题主要考查两个平面垂直的性质、直线与平面所成角等有关知识，以及逻辑思维能力和空间想象能力.满分12分.

（Ⅰ）证明：如图1，取AC中点D，连结PD、BD.

因为PA=PC，所以PD⊥AC，又已知面PAC⊥面ABC，

所以PD⊥面ABC，D为垂足.

因为PA=PB=PC，所以DA=DB=DC，

可知AC为△ABC的外接圆直径，因此AB⊥BC.

（Ⅱ，理科）解：如图2，作CF⊥PB于F，连结AF、DF.

因为△PBC≌△PBA，所以AF⊥PB，AF=CF.

因此，PB⊥平面AFC，

所以面AFC⊥面PBC，交线是CF，

因此直线AC在平面PBC内的射影为直线CF，

∠ACF为AC与平面PBC所成的角.

在Rt△ABC中，AB=BC=2，所以BD=

在Rt△PDC中，DC=

在Rt△PDB中，

在Rt△FDC中，所以∠ACF=30°.

即AC与平面PBC所成角为30°.

（2，文科）解：因为AB=BC，D为AC中点，所以BD⊥AC.

又面PAC⊥面ABC，

所以BD⊥平面PAC，D为垂足.

作BE⊥PC于E，连结DE，

因为DE为BE在平面PAC内的射影，

所以DE⊥PC，∠BED为所求二面角的平面角.

在Rt△ABC中，AB=BC=，所以BD=.

在Rt△PDC中，PC=3，DC=，PD=，

所以

因此，在Rt△BDE中，，

所以侧面PBC与侧面PAC所成的二面角为60°.

18．[2004年全国高考(甘肃贵州青海宁夏新疆)理科数学第20题，文科数学第21题]

本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析

问题能力.满分12分

解：（Ⅰ）如图1，取AD的中点E，连结PE，则PE⊥AD.

作PO⊥平面在ABCD，垂足为O，连结OE.

根据三垂线定理的逆定理得OE⊥AD，

所以∠PEO为侧面PAD与底面所成的二面角的平面角，

由已知条件可知∠PEO=60°，PE=6，

所以PO=3，四棱锥P—ABCD的体积

VP—ABCD=

（Ⅱ）解法一：如图1，以O为原点建立空间直角坐标系.通过计算可得

P（0，0，3），A（2，－3，0），B（2，5，0），D（－2，－3，0）

所以

因为所以PA⊥BD.

解法二：如图2，连结AO，延长AO交BD于点F.通过计算可得EO=3，AE=2，

又知AD=4，AB=8，

得

所以Rt△AEO∽Rt△BAD.

得∠EAO=∠ABD.

所以∠EAO+∠ADF=90°

所以AF⊥BD.

因为直线AF为直线PA在平面ABCD 内的身影，所以PA⊥BD.

19．（2004年北京高考·文史第16题，本小题满分14分）

本小题主要考查直线与平面的位置关系、棱柱等基本知识，考查空间想象能力、逻辑思维能力和运算能力。满分14分。

解：（I）正三棱柱的侧面展开图是长为6，宽为2的矩形

其对角线长为

（II）如图，将侧面绕棱旋转使其与侧面在同一平面上，点B运动到点D的位置，连接交于M，则就是由顶点B沿棱柱侧面经过棱到顶点C1的最短路线，其长为

故

（III）连接DB，，则DB就是平面与平面ABC的交线

在中

又

由三垂线定理得

就是平面与平面ABC所成二面角的平面角（锐角）

侧面是正方形

故平面与平面ABC所成的二面角（锐角）为

20．（2004年北京高考·理工第16题）

本小题主要考查直线与平面的位置关系、棱柱等基本知识，考查空间想象能力、逻辑思维能力和运算能力。满分14分。

解：（I）正三棱柱的侧面展开图是一个长为9，宽为4的矩形，其对角线长为

（II）如图1，将侧面绕棱旋转使其与侧成在同一平面上，点P运动到点的位置，连接，则就是由点P沿棱柱侧面经过棱到点M的最短路线

设，则，在中，由勾股定理得

求得

（III）如图2，连结，则就是平面NMP与平面ABC的交线，作于H，又平面ABC，连结CH，由三垂线定理得，

就是平面NMP与平面ABC所成二面角的平面角（锐角）

在中，

在中，

故平面NMP与平面ABC所成二面角（锐角）的大小为

立体几何高考题

今年的全国高考数学选择题中出了两道有关建筑的题目，一道是埃及胡夫金字塔，另一道则是我们所熟知的天坛。两道题都是以知名建筑作为材料引入，但是本质上都是考的数学计算，但是也千万不要小瞧这两道题，如果考生的空间想象力不够，想要做对这两道题还是有一定的难度的，下面我们就一起来看一下这两道题，看一下到底有多难。

第一道题就是埃及胡夫金字塔，题目中有提到它的形状可以视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥的一个侧面三角形的面积，问侧面三角形底边上的高与底面正方形边长的比值？这道题是一个立体几何题，要想做对这道题考场上可以画一个简图，不需要特别精确你能看懂就行，毕竟考场时间最重要，比如下面这个。

其实这道题没有太大难度，只要把题目读懂就能列出方程，第一个方程要用到勾股定理，第二个方程要用到面积相等。为了简便计算我们可以设正四棱锥底边长为2，这里解释一下为什么要设为2？其实不设成2也可以，你设成1、4、?、x、b这些数都可以，因为最后结果是一个比值，你不管设成什么最后都会被约掉。如果你题目做得多了一眼就能看出设边长为2最简单，因为一半刚好是1，后面进行计算的时候1的平方还是1，这样能节约很多计算的时间。作为一个选择题不要自己给自己找麻烦，能快速做出答案就可以。最后上面那两个式子合并之后就能得到一个一元二次方程，解出来之后有两个解，一个负数舍掉，然后再比上边长2就是正确答案C！这道题的难度有两点，一能不能画出图形，二能不能列出上面两个式子并解出来。

接下来是全国二卷的选择第4题，考的是天坛最后问的是三层共有扇面型石板多少块？高考题确实是有一定难度的，但是考试也不能太着急，一定要仔细花时间读题，把题目中的关系理清楚。高考题的4个选项中就算错误答案也不是随便给的，有同学问我刚好算错而且选项中还有错的这个答案，怎么这么巧？这不是巧合，出题老师在出题设置四个选项的时候就已经考虑到了学生可能算错的情况有哪些，可能会算出来什么答案。

我们开始看这道题，先看最上面一层，第一环是9块，向外每环增加9块第二环就应该是18，第三环应该就是27，这是一个公差为9等差数列，求和公式Sn如上图，这个求和公式不做过多解释，假设看到这里的同学已经学完了所有高中知识。因为每一层的环数相同，所以第二环的石板个数应该是第二个大圆减去第一个小圆即S2n-Sn，同理最下面的那一环石板个数用第三个大圆减去第二个圆即S3n-S2n，这三组公式又组成了等差数列，公差为n^2d，平常做的题多了应该很容易记住这个二级结论，不会也没关系考场的是可以推出来的。所以由题意可得729=公差=n^2d，d=9，n=9，也就是一共有九环。然后我们把三个式子加起来就是3402，其实这道题你也可以完全把这个天坛拍扁，就看成平面上的三个同心圆，就是S3n本身。因此这道题的答案是3402，选择C。这道题本身是有难度的，个人感觉比金字塔要难一些，这道题你做对了吗？

1)由余弦定理求得DB=√6*AD=√6*AB/2

PB=√（PD）∧2+（DB）∧2=

PA=√（PD）∧2+（AD）∧2=

用勾股定理，证明三角形PAB是直角三角形即可，即只要PA∧2+AB∧2=PB∧2即可

2)设D点在三角形BPC的垂足为F点，用第一问的方法求出三角形PFD是直角三角形即可求出